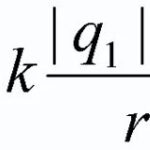Sähköpotentiaalin käsite on yksi sähköstaattisen ja sähködynamiikan teorian tärkeimmistä perusteista. Sen olemuksen ymmärtäminen on välttämätön edellytys näiden fysiikan alojen jatkotutkimukselle.
Sisältö
Mikä on sähköpotentiaali
Asetetaan kiinteän maksun Q luomaan kenttään yksikkömaksu q, johon vaikuttaa Coulombin voima F=k*Qq/r.
Tässä ja alla k=((1/4)*π* ε* ε), jossa ε0 — sähkövakio (8,85*10-12 F/m), kun taas ε on keskimääräinen dielektrisyysvakio.
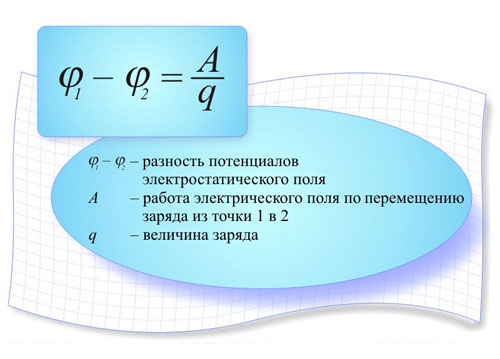
Osallistunut veloittaa tämän voiman vaikutuksesta se voi liikkua, ja voima tekee tietyn määrän työtä. Tämä tarkoittaa, että kahden varauksen järjestelmällä on potentiaalienergia, joka riippuu molempien varausten suuruudesta ja niiden välisestä etäisyydestä, eikä tämän potentiaalisen energian suuruus riipu varauksen q suuruudesta. Tässä esitetään sähköpotentiaalin määritelmä - se on yhtä suuri kuin kentän potentiaalienergian suhde varauksen suuruuteen:
φ = W/q,
missä W on varausjärjestelmän luoman kentän potentiaalienergia ja potentiaali on kentän energiaominaisuus. Varauksen q siirtämiseksi sähkökentässä jonkin matkan verran, on tarpeen käyttää tietty määrä työtä Coulombin voimien voittamiseksi. Pisteen potentiaali on yhtä suuri kuin työ, joka on käytettävä yksikkövarauksen siirtämiseksi tästä pisteestä äärettömään. Tätä tehdessä on huomattava, että:
- tämä työ on yhtä suuri kuin varauksen potentiaalienergian lasku (A=W2-W1);
- työ ei riipu latauksen liikeradalta.
SI-järjestelmässä potentiaalin yksikkö on yksi voltti (venäläisessä kirjallisuudessa sitä merkitään kirjaimella V, ulkomaisessa kirjallisuudessa - V). 1 V \u003d 1J / 1 C, eli voimme puhua 1 voltin pisteen potentiaalista, jos 1 C:n varauksen siirtämiseen äärettömyyteen kuluu 1 Joule. Nimi valittiin italialaisen fyysikon Alessandro Voltan kunniaksi, joka antoi merkittävän panoksen sähkötekniikan kehitykseen.
Potentiaalin visualisoimiseksi sitä voidaan verrata kahden kappaleen lämpötilaan tai avaruuden eri pisteissä mitattuun lämpötilaan. Lämpötila mittaa esineiden lämpenemistä ja potentiaali on sähkövarauksen mitta. Sanotaan, että yksi kappale kuumenee enemmän kuin toinen, voidaan myös sanoa, että yksi kappale on varautunut enemmän ja toinen vähemmän. Näillä elimillä on erilaiset mahdollisuudet.
Potentiaalin arvo riippuu koordinaattijärjestelmän valinnasta, joten vaaditaan jokin taso, joka on otettava nollaksi. Lämpötilaa mitattaessa perusviivaksi voidaan ottaa esimerkiksi jään sulamisen lämpötila.Potentiaalille nollatasoksi otetaan yleensä äärettömän kaukana olevan pisteen potentiaali, mutta joidenkin ongelmien ratkaisemiseksi esimerkiksi maapotentiaalia tai jonkin kondensaattorilevyn potentiaalia voidaan pitää nollana.
Mahdolliset ominaisuudet
Potentiaalin tärkeistä ominaisuuksista on huomattava:
- jos kentän muodostavat useat varaukset, niin potentiaali tietyssä pisteessä on yhtä suuri kuin kunkin varauksen synnyttämien potentiaalien algebrallinen summa (ottaen huomioon varauksen etumerkki) φ=φ1+φ2+φ3+φ4+φ5+…+φn;
- jos etäisyydet varauksista ovat sellaiset, että itse varaukset voidaan pitää pistevarauksina, niin kokonaispotentiaali lasketaan kaavalla φ=k*(q1/r1+q2/r2+q3/r3+…+qn/rn), missä r on etäisyys vastaavasta varauksesta sitten tarkasteltavan pisteen.
Jos kentän muodostaa sähködipoli (kaksi kytkettyä vastakkaisen etumerkin varausta), niin potentiaali missä tahansa etäisyydellä r dipolista sijaitsevassa pisteessä on yhtä suuri kuin φ=k*p*cosά/r2, missä:
- p on dipolin sähköinen käsivarsi, yhtä suuri kuin q*l, missä l on varausten välinen etäisyys;
- r on etäisyys dipolista;
- ά on dipolivarren ja sädevektorin r välinen kulma.
Jos piste on dipolin akselilla, niin cosά=1 ja φ=k*p/r2.
Mahdollinen eroavaisuus
Jos kahdella pisteellä on tietty potentiaali, ja jos ne eivät ole yhtä suuret, he sanovat, että näiden kahden pisteen välillä on potentiaaliero. Potentiaaliero esiintyy pisteiden välillä:
- jonka potentiaali määräytyy erimerkkisten varausten perusteella;
- piste, jonka potentiaali on minkä tahansa etumerkin varauksesta, ja piste, jonka potentiaali on nolla;
- pisteitä, joilla on saman merkin potentiaali, mutta jotka eroavat absoluuttiselta arvoltaan.
Eli potentiaaliero ei riipu koordinaattijärjestelmän valinnasta.Voidaan vetää analogia vesialtaista, jotka sijaitsevat eri korkeuksilla suhteessa nollamerkkiin (esimerkiksi merenpinnan tasoon).
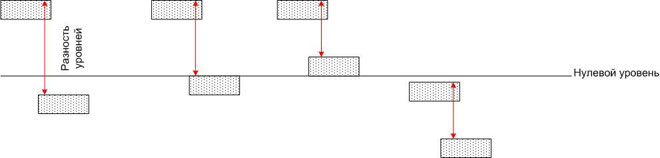
Jokaisen altaan vedellä on tietty potentiaalienergia, mutta jos yhdistät mitkä tahansa kaksi allasta putkella, niin jokaisessa niistä tulee vesivirta, jonka virtausnopeus ei määräydy pelkästään putken koon mukaan. , mutta myös Maan gravitaatiokentän potentiaalienergioiden erolla (eli korkeuserolla). Potentiaalisten energioiden absoluuttisella arvolla ei ole tässä tapauksessa merkitystä.
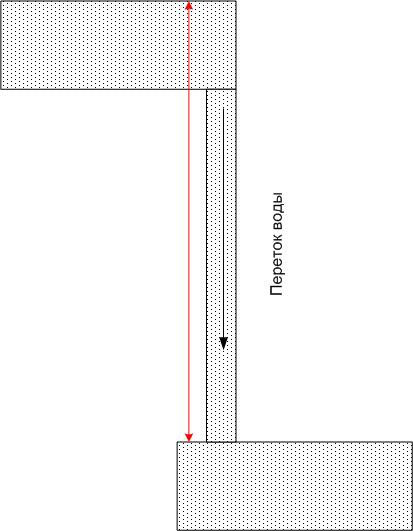
Samalla tavalla, jos yhdistät kaksi pistettä, joilla on eri potentiaali johtimella, se virtaa sähköä, joka määräytyy paitsi johtimen resistanssin, myös potentiaalieron (mutta ei niiden absoluuttisen arvon) perusteella. Jatkamalla analogiaa veden kanssa, voimme sanoa, että ylemmän altaan vesi loppuu pian, ja jos ei ole voimaa, joka liikuttaisi vettä takaisin ylös (esimerkiksi pumppu), niin virtaus pysähtyy hyvin nopeasti.
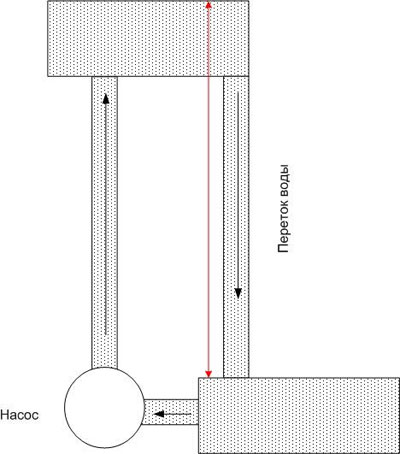
Näin on sähköpiirissä - potentiaalieron ylläpitämiseksi tietyllä tasolla tarvitaan voimaa, joka siirtää varauksia (tarkemmin sanottuna varauksenkuljettajia) pisteeseen, jossa on suurin potentiaali. Tätä voimaa kutsutaan sähkömoottorivoimaksi ja siitä käytetään lyhennettä EMF. EMF voi olla luonteeltaan erilainen - sähkökemiallinen, sähkömagneettinen jne.
Käytännössä tärkeintä on lähinnä varauksenkuljettajien liikeradan alku- ja loppupisteiden välinen potentiaaliero. Tässä tapauksessa tätä eroa kutsutaan jännitteeksi, ja SI:ssä se mitataan myös voltteina.Voimme puhua 1 voltin jännitteestä, jos kenttä tekee 1 joulen työtä siirrettäessä 1 Coulombin varausta pisteestä toiseen, eli 1V \u003d 1J / 1C, ja J / C voi olla myös mahdollinen eroavaisuus.
Potentiaalien tasauspinnat
Jos useiden pisteiden potentiaali on sama ja nämä pisteet muodostavat pinnan, niin tällaista pintaa kutsutaan ekvipotentiaaliksi. Tällaisella ominaisuudella on esimerkiksi sähkövarauksen ympärille rajattu pallo, koska sähkökenttä pienenee etäisyyden myötä tasaisesti kaikkiin suuntiin.
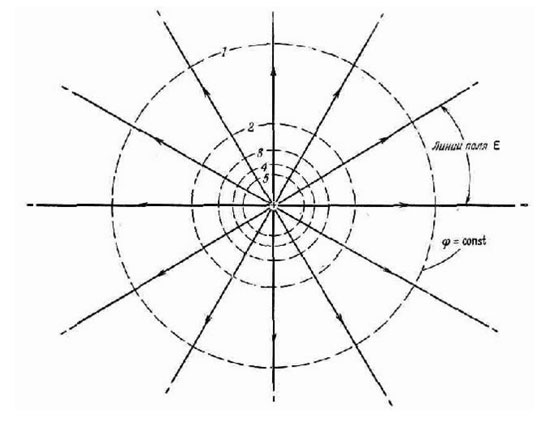
Kaikilla tämän pinnan pisteillä on sama potentiaalienergia, joten kun varausta siirretään tällaisen pallon yli, työtä ei käytetä. Useiden varausten järjestelmien ekvipotentiaalipinnat ovat muodoltaan monimutkaisempia, mutta niillä on yksi mielenkiintoinen ominaisuus - ne eivät koskaan leikkaa. Sähkökentän voimalinjat ovat aina kohtisuorassa pintoihin, joilla on sama potentiaali kussakin pisteessään. Jos ekvipotentiaalipinta leikataan tasolla, saadaan yhtäläisten potentiaalien viiva. Sillä on samat ominaisuudet kuin potentiaalintasaisella pinnalla. Käytännössä esimerkiksi sähköstaattiseen kenttään sijoitettujen johtimen pinnalla olevien pisteiden potentiaali on yhtä suuri.
Kun olet käsitellyt potentiaalin ja potentiaalieron käsitettä, voit jatkaa sähköilmiöiden jatkotutkimusta. Mutta ei aikaisemmin, koska ilman perusperiaatteiden ja käsitteiden ymmärtämistä ei ole mahdollista syventää tietoa.
Samanlaisia artikkeleita: